기계 학습: T라는 작업의 기존 P성능을 학습 E를 통해 성능이 개선되는 것을 학습한다고 말한다.
분류(Classification): 미리 정의된 범주에 입력 데이터를 할당하는 문제 (범주 O)
군집화(clustering): 미리 정의된 규칙에 따라 데이터를 그룹화하는 문제
기계학습 방법론
* 지도학습, 비지도학습, 반지도학습
1. 지도학습
정답이 부착된 데이터(Label)를 바탕으로 학습 진행
[장점] 비지도 학습에 비해 높은 성능을 보인다.
[단점] 데이터 구축에 많은 시간과 노력이 필요하다.
예시 : 기사 분류, 영화평 예측(긍정, 부정), 기계 독해, 기계 번역, 챗봇 등 정답이 있는 레이블
2. 비지도학습
정의된 척도(Measure)에 따라 학습 진행
[장점]데이터 구축이 쉽다.(정답 부착 불필요)
[단점]지도 학습에 비해 낮은 성능
예시 : 유클리디언 거리, 코사인 유사도/ 유사한 문장, 문서들 그룹화, 비슷한 의미의 단어들 그룹화
3. 반지도학습
소량의 정답 부착 데이터를 바탕으로 모델을 만들고
대량의 정답 미부착 데이터를 활용하여 성능을 개선하는 방향으로 학습을 진행
[장점] 데이터 구축이 지도학습보다 쉬움
[단점]지도학습에 비해 낮은 성능, (but, 근접한 성능]
성능 : 지도학습 >> 반지도학습 ? 비지도 학습
구축 비용: 지도학습 > 반지도학습 ? 비지도학습
데이터 구성
[훈련 데이터(train) 8: 개발데이터 (Validation) 1: 평가 데이터 (test) 1]
훈련 데이터(모델 개발 단계)
: 모델을 만들기 위해 사용되는 데이터
개발 데이터(모델 개발 단계)
: 학습이 잘되고 있는지 평가하는데 사용되는 데이터
훈련 데이터에 속하지 않는 데이터에서도 잘 작동하는지 테스트
평가 데이터 (정확도 평가 측정)
: 최종 학습된 모델을 평가하기 위해 사용되는 데이터
지도학습 모델 개발 절차
데이터 수집 -> 데이터 변환( 피처추출, 정답 부착) ->모델 학습 -> 모델 평가
데이터 수집
1) 기계학습 대상이 되는 문제를 명확히 선정
2) 문제 해결을 위한 데이터를 가능한 많이 수집
3) 문제 대상 데이터(positive)와 비대상 데이터(negative)를 균형 있게 수집 (5:5, 6:4, 7:3 등)
데이터 변환
1) 정답 부착 (Labeling, tagging, annotation)
지도 학습을 위해서 자질 추출 데이터에 정답을 부착하는 작업
매우 중요한 과정이며 시간과 노력이 많이 든다.
2) 자질추출 (Feature Extraction)
주어진 문제를 해결하는데 중요한 단서가 될 수 있는 정보를 선별하여 기계가 읽을 수 있는 형태로 변환하는 작업 (엔지니어의 능력이 중요하다.)
모델 학습
1) 주어진 문제에 적합한 모델 선택 ( ML / DL)
2) 다양한 툴깃을 이용하여 모델 구성 및 학습
모델 평가 (3가지 다 해야함)
1) Closed Set ( => train set의 loss 감소해야한다.)
학습 데이터를 이용한 평가
학습이 되고 있는지 단순 확인한느 과정
2) Development test (Dev set)
학습에 참여하지 않은 데이터에서 잘 작동하는지, 올바른 방향으로 학습되고 있는지를 확인하는 과정
3) Open test
학습에 참여하지 않은 데이터를 이용한 평가
실제 환경에서 어느 정도 성능이 나오는지 확인하는 과정
모델 평가 방법 예시
1. 10배 교차검증 : 10-fold cross validation
A. 데이터를 10등분
B. 9개로 학습하고 나머지 1개로 평가 ( train : test = 9:1 => 10번 평가)
C. 10회의 평가의 평균 값을 모델의 성능으로 사용한다.
D. 목적 : 예측값에 대한 오차를 줄이기 위해 사용한다.
2. 평가 척도 ( Evaluation measure)
A. 정밀도(Accuracy) : 모델의 출력들 중에 맞은 것의 비율
B. 정확률(Precision) : 범주 별(레이블 별) 모델의 출력 중에 맞은 것의 비율
C. 재현율(recall) : 범주 별(레이블 별) 정답 중에 모델이 맞춘 것의 비율
D. F1-score : 정확률과 재현율의 조화평균
Hypothesis: '어떤 문제일 것이다’라고 가정하고 규칙을 찾는 것이다.
Linear Hypothesis 근접한 직선의 방정식 찾기, 무수히 많은 직선 중 가장 적절한 직선 찾기.
H(x) = Wx + b
목표 : 최적의 W와 b 찾기
방법 : H(x)와 실제 값(y)의 오차가 가장 작은 선 찾기 : cost function
Cost Function
비용함수: 예측 값 – 실제 값 = error, 이 error의 합이 가장 낮은 것을 찾는 게 목표
1) Linear : MSE(평균 제곱오차) 비용함수

2) Logistic : Sigmoid 비용함수
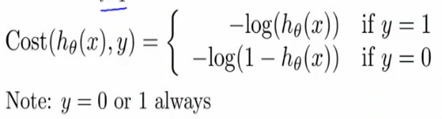
: 0과 1로 무조건 출력
Gradient Decent : 경사 하강법
기계학습은 cost function을 바탕으로 기울기를 계산한다.
기울기 값이 크면 큰 범위로 x값을 변경하고
기울기 값이 작으면 작은 범위로 변경하여 기울기를 0으로 만든다.
이때 기울기가 0이 된 W값이 cost function의 최소이다.
기울기 음수 : W 증가 / 기울기 양수 : W 감소 [기울기 : cost function 미분 값, W: 입력 값]
Epoch
: 학습을 위한 데이터 전체를 모두 읽었을 때, epoch 1회.
Batch
: 데이터가 클 경우 메모리 초과로 인해 1 epoch 하기 어려운 경우에 사용한다.
batch의 크기만큼 데이터를 가져와서 데이터를 읽고 다음 batch를 읽는다.
[예시]
Epoch 1 = batch1(100개 데이터) + batch2(100개 데이터) + …. + batch10(100개 데이터)
이걸 50번하면, epoch 50이다.
Decision Tree
Decision Tree(결정 트리)는 자질(Features)들의 정보 획득량(information gain)에 따라 트리 형태의 규칙을 자동 생성하는 기계학습 모델이다.
[장점]
피처 선택을 하지 않아도 됨.
빠르게 학습한다.
해석가능한 결정 규칙이 있고, 규칙을 변경할 수 있다.
(딥러닝은 해석 불가하기 때문에 설명가능한 ai: XAI가 발전하는 이유이다.)
다른 타입의 피처를 다룰 수 있다.
[단점]
피처를 결합하지 못하고 독립적으로 계산한다.
(보완) 피처 결합하여 새로운 피처를 데이터에 넣어준다. (피처 재디자인)
한번 사용한 피처는 아래에서 다시는 고려하지 않는다.
* 자질(Features)
- 문제 해결에 영향을 미치는, 판단 근거가 되는 요소
- 관측 및 측정 가능한 요소 (피처를 잘 선정하는 것이 기계학습 전문가의 역량)
[고려 사항]
- 연속 피처(continuous feature)
: 엔트로피 측정을 위해서는 이산 자질(discrete feature)로 변환 해야한다.
Ex: 기온 < 15 : cool / 15 < 기온 <25 : mild / 25 < 기온 : hot
- 복잡한 피처
- 비싼 피처
* 정보 획득량 (Information Gain)
- 자질의 값을 알게 됨으로써 얻어지는 문제 복잡도(전체 엔트로피)에 대한 감소 기대치
감소 기대치 : 어떤 피처(정보)를 선택해야 해당 문제가 얼마나 쉬워질지
Ex) 내일 시험 볼까? -> 정보 획득[조교가 내일 시험 안 본대 / 교수님이 시험 본대 ]
-> 교수님의 말 선택 -> 복잡도 감소
- 엔트로피
문제의 복잡도를 측정하는 척도 è 얼마나 복잡한지 측정
- 정보이론 : 특정확률 p를 가진 메시지를 상대방에게 전달하는데 필요한 비트 수에 대한 기대값
- 엔트로피 최대값
가장 애매한 확률(0.5) 을 가질 때 판단을 내리기 가장 힘들다
è 문제가 복잡하다 è 최대 엔트로피이다.
기대 값: 각 사건이 발생할 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값.

엔트로피 공식 : log_2 : bit값 계산
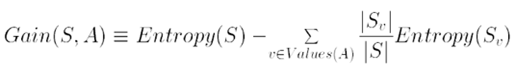
감소 기대치(정보 획득량) = 피처 값 모를 때 엔트로피 – 피처 값 알게 되었을 때 엔트로피 => 클수록 좋다.
Support Vector Machine ( SVM)
: 데이터들을 커널함수를 이용하여 고차원 공간으로 사상시킨 후
support vector(지지벡터)들로 이루어진 초평면을 이용하여 선형 분류하는 마진 기반 기계학습 모델이다.
* Deep Neural Network 나오기 전 가장 유용하게 사용했다.
* 비선형분류 문제를 고차원 선형분류 문제로 바꾸는데 사용한다.
커널 함수
1) 저차원 데이터를 고차원 공간으로 사상(mapping) 시키는 함수이다.
2) [기능] 선형 분리 불가능한 문제를 선형 분리 가능 문제로 변환한다.
선형 분리 가능 문제 : 한 개의 직선(초평면)으로 분리할 수 있는 문제.
지지 벡터 (Support Vector)
1) 선형분류의 경계 주변에 존재하는 데이터 포인트들이다.
2) 이진 선형 분류 문제에서는 수많은 support vector들이 존재한다.
최대마진
1) 선형 분류를 가능하게 하는 직선은 무수히 많이 존재한다.
2) 그 중에서 마진을 최대로 하는 직선이 가장 이상적이다.
3) 마진: 선을 기준으로 support vector들 사이의 거리의 합이다.
커널트릭
1) SVM함수는 고차원 공간에서의 내적을 통해서 구현
2) 고차원 공간으로 사상하고 내적을 구하는 것은 매우 복잡하다. 따라서 현재 차원에서 동일한 효과를 거두는 커널 함수를 사용하는데 이를 커널 트릭이라고 한다. (같은 공간에서 옮겨주는 것.)
3) [예시] Polynomial, Radial Basis function, sigmoid
SVM에 적합한 문제
- 선형 분류 문제 : DT = NN = SVM
- 비선형 분류 문제 : NN >= SVM
비선형 분류 문제 à 고차원에서의 선형 분류 문제 : SVM >>= DT, NN
Linear hypothesis 문제 중 가장 좋은 성능을 푸는 건 SVM이다.
Statistical Models (HMM)
HMM( Hidden Markov Model)
Hmm = Hidden + Markov Model
Markov Model
1) Sequence Probability / transition probability만 존재.
2) 어떤 상태에서 어떻게 변해가는지 전이되는 확률 값을 가진 모델이다.
3) 학습데이터로부터 얻어진 전이(transition) 확률분포
(상태 간 이동 확률 분포: 앞의 상태를 보고 이에 따른 판단에 따름.)
4) 결합 확률(joint probability) 계산 모델
5) 연쇄 규칙과 마코프 가정을 이용하여 결합 확률을 단순화하여 결합 확률을 근사화 시키는 모델이다.
6) State가 정해져있고 transition probability(전이 확률: 상태 à 상태 변경될 확률)계산
7) 앞의 상태 1개만 보면, 1차 마코프모델 ( bi-gram model)
앞의 상태 2개 보면, 2차 마코프모델 ( tri-gram model)
(이때, 앞의 보는 상태가 많아지면 훈련 데이터가 많아야 한다.)
HMM : Hidden Markov Model
1) 풀고자 하는 레이블(상태)를 직접 관측할 수 없는 상황에서
상태를 예측하는데 도움이 되는 특징(자질, feature)만을 관측할 수 있다.
2) 직접 관측할 수 없는(상태가 감춰져 있는) 상황에서 확률로만 존재.
3) 상태 : 전이 확률(transition probability)과
관측: 관측 확률(Observation Probability)가 존재한다.
문제 : 특정 피처를 관측했을 때, 해당 상태를 예측하는 것.
4) 전이확률, 관측확률의 곱의 합이 가장 큰 확률을 갖는 Lable 리턴
5) [예시] 날씨(레이블)를 관측할 수 없을 경우 신발(특징, feature) 관측을 통해 날씨 예측
[장화, 운동화] 신을 경우: 각 [날씨 확률]
Sequence Labeling Problem
=> 상당히 많은 부분. / 기존의 classification 과 다른 것.
=> 시간 축으로 따라 들어온 입력들에 대해 시간축마다 분류하는 것.
=> 시간 축에 따라 끊임없이 뒤에 영향을 미쳐가면서 분류해 나가는 것.
=> Viterbi 알고리즘을 사용해서 각 상태마다 가장 큰 확률 값을 남겨
모든 경로를 고려하지 않고도 빠른 시간 내에 최적의 경로를 찾는다.
최종 path에 대해 각 상태에 맞는 label을 출력함.
Statistic Models
각 그래프 방향에 따라 어떤 모델인지 구분.
HMM 히든 마콥모델 (결합확률 모델)
1) 전이확률과 관측확률의 곱에 의해 표현된다.
2) joint probability에 의해 Chain rule 생성된다
3) 90년대 말까지 sequence labeling 문제 풀었음.
4) [문제점] 우리가 풀고자 하는 문제는 X를 관측한 후 Y를 예측하는 것이지만, HMM은 y로부터 x를 계산한다. 이때 독립가정을 해야 하는 문제가 생김. è 놓치는 경우가 많은 문제 발견. (Observation에 대해 많은 bias가 존재한다.)
1) Independence assumption 문제
2) Observation Bias 문제

Linear Hypothesis problem : SVM 모델
Sequence Labeling Problem : CRFs 모델
MEMM : 방향성 조건부 확률 모델 : Maximum Entropy Markov Model)
1) 엔트로피를 최대화하는 마코브 모델
2) 관측되지 않은 피처에 대해 동일한(even) 확률 값을 주자 è 엔트로피가 높아진다.
3) 90년 후반 ~ 2000년 초반까지 각광 ( HMM보다 성능 더 좋음)
4) [문제점] Transition Probability에 문제가 있다.
è Label bias 문제발견
: local normalize로 인해 실제 값이 작은 경우에도
해당 상태에서 다음 상태로 전이 확률의 값이 커진다.
이러한 문제 해결하기 위해 Global normalize해서 무방향성으로 해야겠다.

CRFs 무방향성 조건부 확률 모델 (Conditional Random fields)
1) MEMM의 Label bias문제를 완화하기 위해 무방향성으로 변경한 모델
2) 기존 Local Normalize는 전이가 많은 상태는 항상 불리하기 때문에
Global Normalization을 통해 모든 상태를 기준으로 정규화 한다. : CRFs의 핵심

HMM이 가지고 있던 문제인 Independence assumption 문제를 MEMM이 해결
MEMM이 가지고 있던 transition Probability 문제를 CRFs가 해결
HMM << MEMM << CRFs : 딥러닝 나오기 전 가장 좋은 확률 모델
인공 신경망(Artificial Neural Network)
ANN(인공신경망)
1) 수학적 논리학이 아닌 인간의 두뇌를 모방하여 수많은 간단한 처리기들(뉴런)의 네트워크를 통해 문제를 해결하는 기계학습 모델이다.
2) Dendrites 수상돌기 : 전기 신호를 받는다, 굵기는 신호를 받을 수 있는 크기에 비례한다.)
3) Cell body : 수상돌기에서 받은 신호를 합친다.
4) Axon(축색돌기) : 합친 전기 신호를 전달한다.
5) Synapse :특정수치 이상이면 신호를 전달한다. (시그모이드 함수를 사용해서 특정 값이 이상이면 전달, 미만이면 전달하지 않는 역할함)
Perceptron (퍼셉트론)
1) 1개의 퍼셉트론은 1개의 선이며, 이 선은 이진 분류기(Binomial Classifier)이다.
2) N개의 퍼셉트론은 n개의 선이며, Multi perceptron으로 다중 분류가 가능해진다.
'Make the Learning Curve > Data Science' 카테고리의 다른 글
| [Random Forest 개요] (0) | 2021.06.04 |
|---|---|
| Text Mining 개요 ( Bow, VSM, TF, IDF, TF-idf , IR) (0) | 2021.04.21 |
| [CNN] CNN을 이용한 MNIST-3 // MNIST Predict (0) | 2020.12.18 |
| [CNN] CNN을 이용한 MNIST-2 // 모델링 (0) | 2020.12.18 |
| [CNN] CNN을 이용한 MNIST-1 // MNIST 이해 및 데이터 확인 (0) | 2020.12.18 |




댓글