1) 랜덤으로 K개 벡터 선택

2) 선택되지 않은 벡터들(검은색)을 선택 된 K개 벡터에 가까운 벡터에 할당(assign)한다.

3) 빨강, 파랑의 벡터들의 centroid를 각 각 계산한다.
-> 빨강색 X(centroid) 지점과 파랑색 X지점을 찾을 수 있다.

4) 위에서 구한 centroid에서 reassign 진행한다.
( 각 각의 centroid에 가까운 벡터들을 assign)
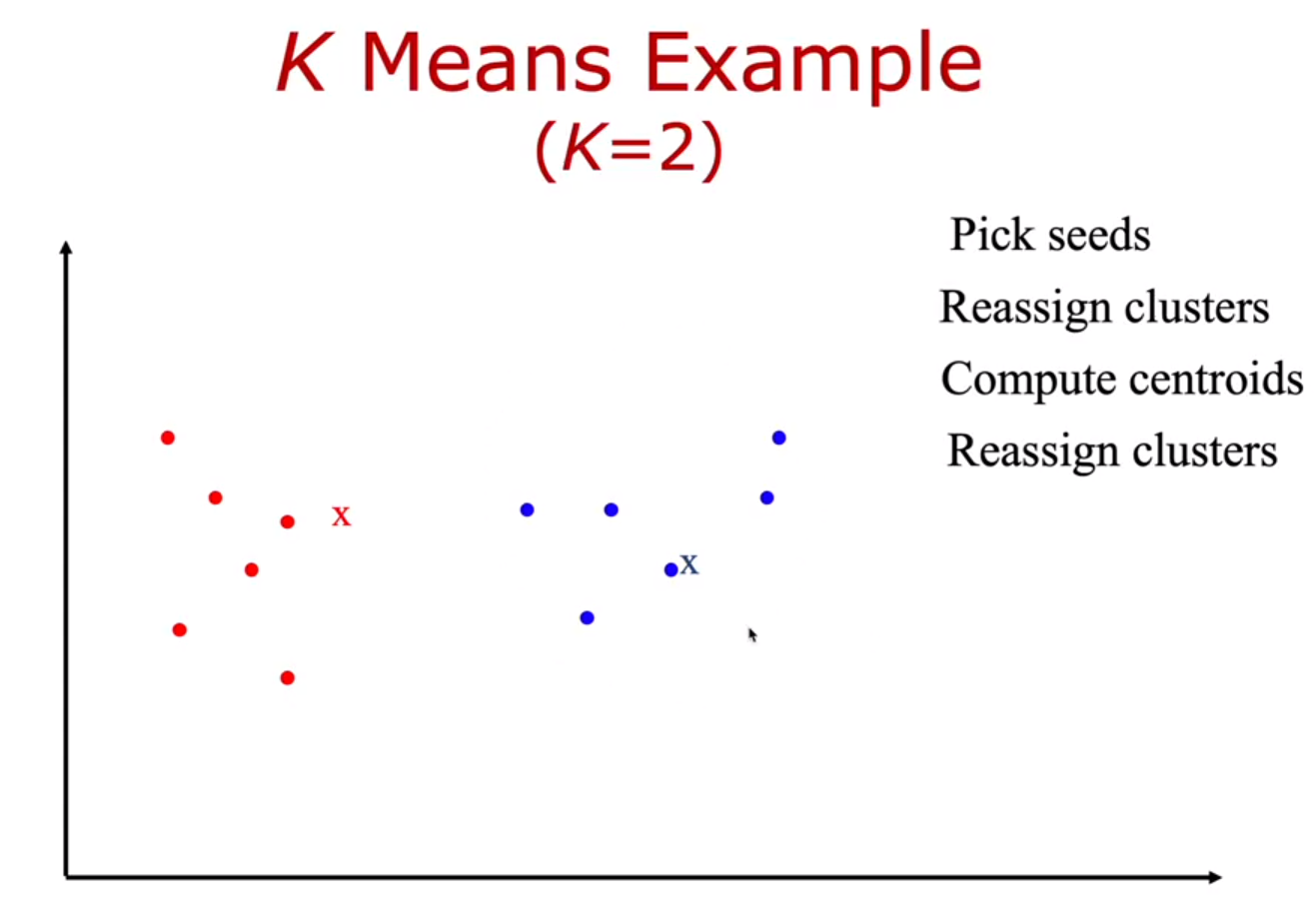
5) reassign한 후 빨강, 파랑의 벡터들의 새로운 centroid를 각 각 계산한다.
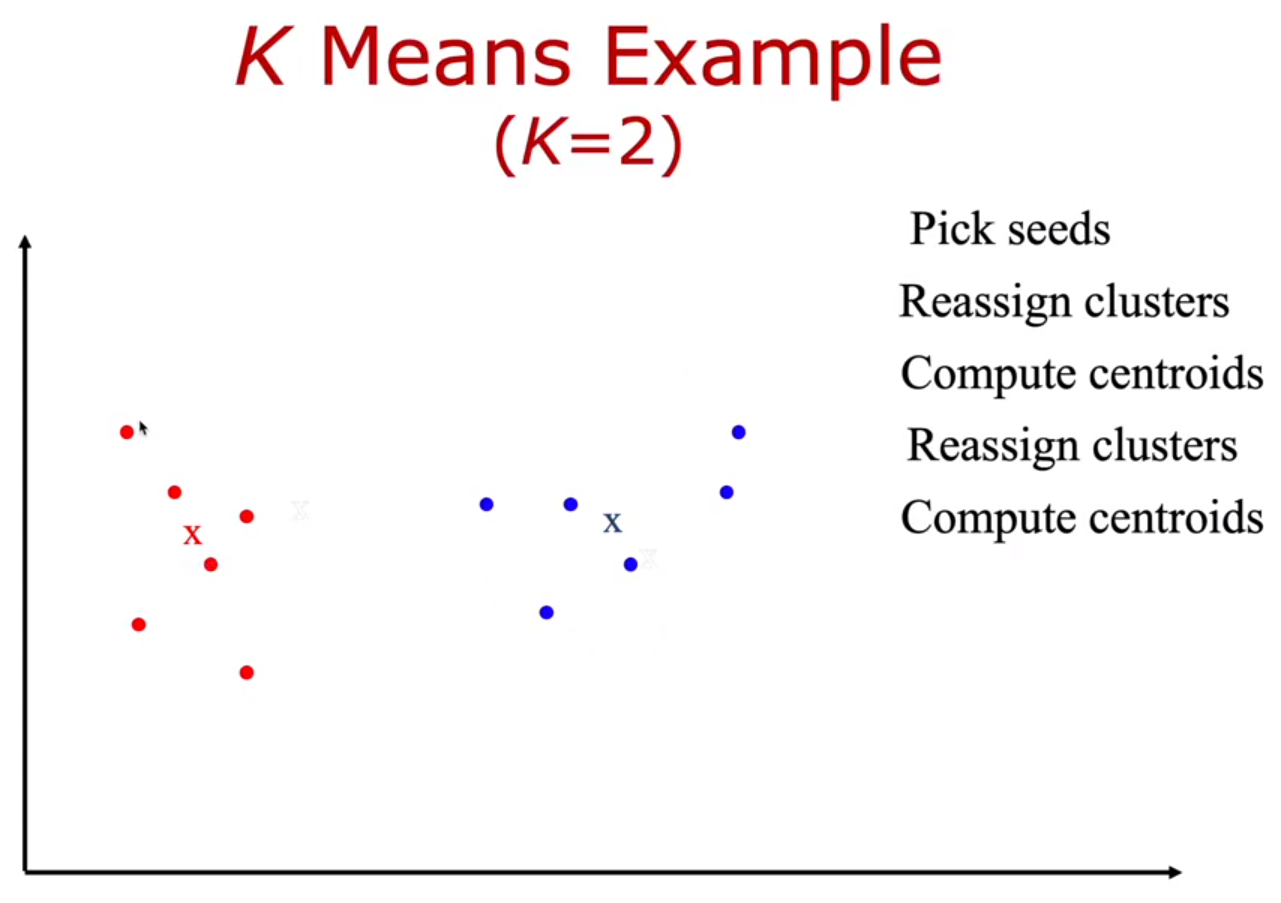
6) 4,5 과정을 계속해서 반복한다.
centroid의 변화가 없을때까지 ( 계속 된 reassign에도 일치되는 centroid 찾을 때까지) 반복한다.
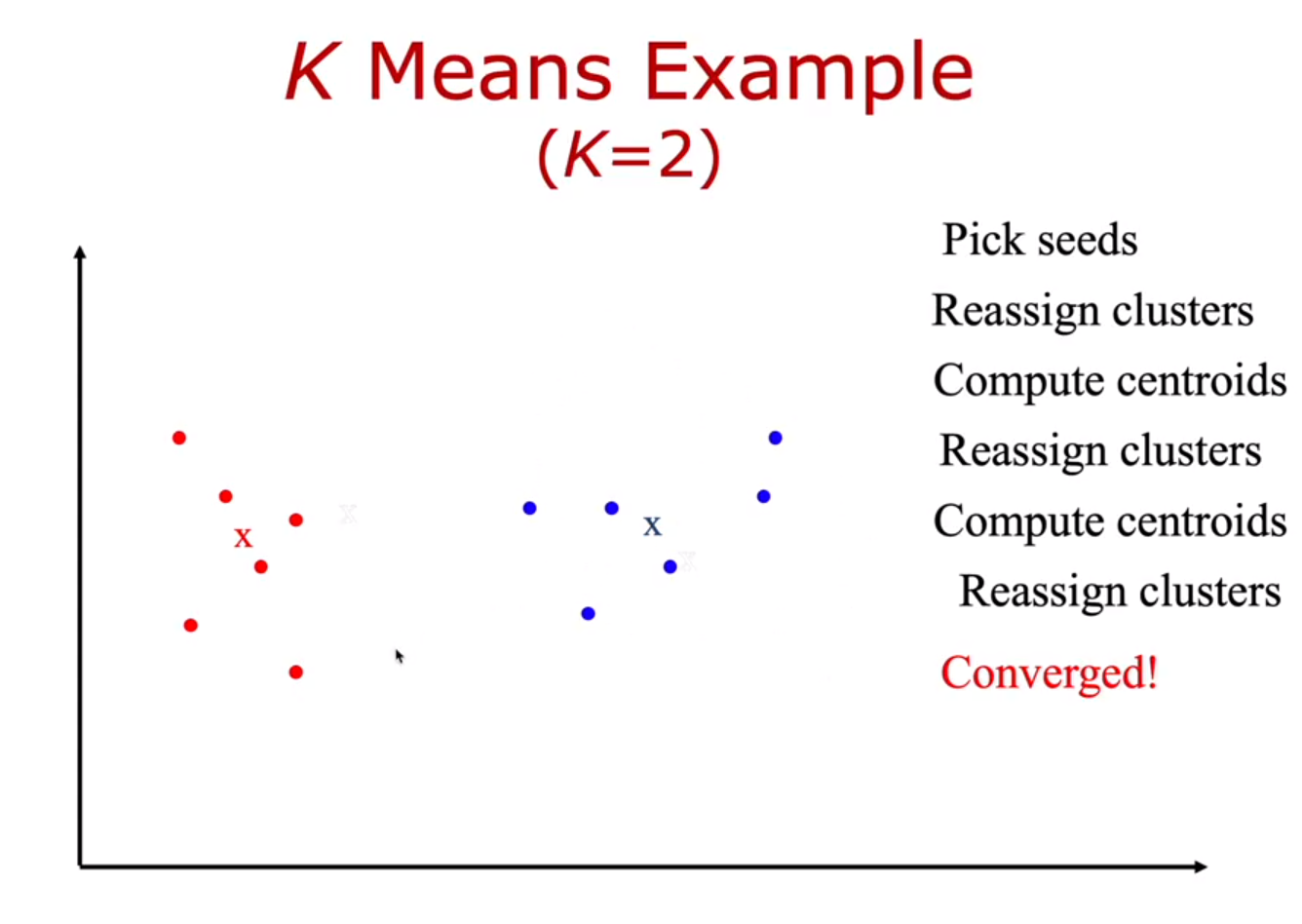
centroid의 변화가 없고 반복이 멈추었다면, 최종으로 두개(k개)의 클러스터로 나눌 수 있다!
따라서 K-Means 알고리즘은
ㄱ) Centroid를 계산하는 단계
ㄴ) 각 데이터의 포인트들을 가장 가까운 centroid에 assign하는 단계
이 두 단계를 loof를 통해 반복하여 최적화 하는 방법이다!

- 그렇다면 언제 이 반복을 종료하는가?
→ 3가지 조건이 있다.
1) 반복 횟수를 설정했을 경우
2) Cluster 내의 Member 변화가 없을 경우
3) Centroid 위치가 변화가 없을 경우
이 경우에 이 loof가 멈추며 반복을 종료한다!
그리고 이제 K-means 알고리즘의 비용함수 (Cost function)을 알아보자.
K-means 알고리즘도 cost function을 정의하고 최소화하는 θ값을 찾아내는 문제이다.
K-means 알고리즘에서 θ 값은 c^(i) , μ_k 이다.
여기서 c^(i) = sample data인 x^(i)가 속해있는 Cluster이고
μ_k= 각 클러스터(K 클러스터)의 centroid(중심) 이다.
그리고 μ_c^(i) = x^(i)가 속한 클러스터 c^(i)의 centroid 이다.
따라서 이러한 파라미터를 가지고 비용함수를 분석해보자.
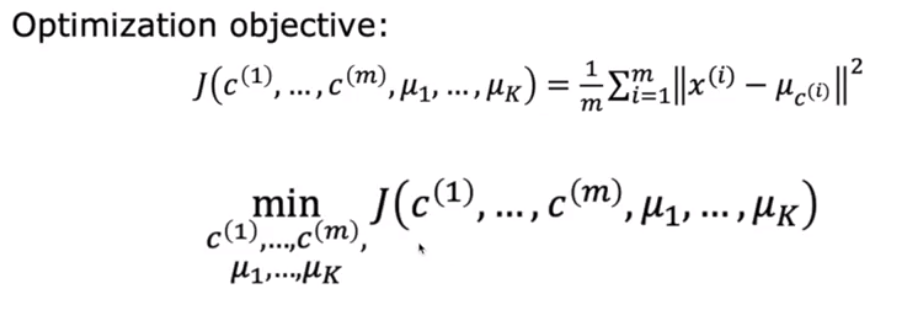
왼쪽이 θ에 의한 함수이고, 오른쪽에 m은 sample data의 개수이다.
그리고 x^(i) - μ_c^(i)의 절댓값 제곱이 있다.
이 오른쪽 항의 의미는
각 데이터 샘플인 x^(i)가 자신이 속한 cluster의 중심으로부터의 유클리디안 거리의 제곱의 합의 평균 이라는 의미이다.
따라서 이 값이 가장 작아야, K-means의 Optimal해가 되는 것이다.
따라서 이를 위해 가장 적절한 θ값( c^(i) , μ_k)을찾아야 한다!
'Make the Learning Curve > Data Science' 카테고리의 다른 글
| [딥러닝] Convolution and Pooling in CNN (0) | 2020.12.12 |
|---|---|
| [딥러닝] Convolutional Neural Network(합성곱 신경망-CNN) 개요 (0) | 2020.12.04 |
| [Deep Learining] 텐서플로우-케라스 신경망을 이용한 선형회귀분석 (0) | 2020.11.30 |
| [Deep Learning] What is D/L? 딥러닝이란? (0) | 2020.11.25 |
| [M/L - Classification]Logistic Regression (feat. Linear Regression) (0) | 2020.11.24 |




댓글